机载传感器辅助实时地形识别系统

2024/10 - 2025/02

本项目结合物理储备计算（Physical Reservoir Computing）与压电传感器，开发了一种低算力、实时地形识别系统。该系统通过轮子自身的振动响应，提取高维特征，实现低功耗、高效的地形分类，适用于火星探测、无人车导航等应用场景。

本研究与NASA JPL合作，并以投稿至IEEE RA-L

主要技术

机械结构设计
- 设计1:4 缩比火星探测车轮毂，采用PLA、PLA-CF、树脂等多材料 3D 打印，优化刚度和稳定性。
- 进行有限元分析（FEA），研究轮辐在不同激励条件下的振动响应，优化传感器布置方案。
传感器集成
- 在轮辐关键位置安装压电传感器，利用其高灵敏度检测轮子与地形的微小振动差异。
- 设计低功耗信号采集电路，结合Shannon 熵、傅里叶变换（FFT）等算法优化地形特征提取。
机器学习识别
- 采用支持向量机（SVM）分类算法，对不同地形特征进行训练，最终识别准确率达 90%。
- 结合欧几里得距离与马哈拉诺比斯距离方法，实现未知地形的智能分类。

研究背景

在火星探测、灾难救援、无人地形探索等任务中，机器人需要对未知环境做出快速决策。然而：

传统视觉传感器（摄像头/LiDAR）：受光照、尘埃、遮挡影响，计算负担大，功耗高。
惯性传感器（IMU）：受累积误差影响，难以精准感知地形特征。
基于力传感的方案：需要机器人直接接触地面，可能影响行驶稳定性。

本研究突破传统视觉/力传感限制，采用“仿生振动感知”，让机器人像蜘蛛腿毛感知振动一样，通过轮子“触摸”地面，分析轮子与地形的接触振动信号，实现高效、低功耗的地形分类。

机械结构设计

为了优化传感器信号采集，研究团队设计并制造了1:4 缩比 Curiosity 火星探测车轮毂，确保其动力学特性尽可能接近真实火星车，以便更准确地模拟地形振动特性。

轮毂结构优化

材料选择：
- 轮毂外壳：PLA（轻量+耐久）
- 轮辐：树脂（高强度+振动稳定性好）
- 轴承连接部位：PLA-CF（碳纤增强）
制造方式：
- 采用多材料 3D 打印技术，确保轻量化与刚度平衡。
- 通过有限元分析（FEA）优化轮毂结构，减少振动信号衰减，提高传感器灵敏度。

基于有限元分析（FEA）的传感器布置优化

在本研究中，为了确保压电传感器能够捕获最具代表性的地形振动信号，采用了有限元分析（FEA）方法，系统性地研究轮毂在不同激励条件下的振动响应，并基于此优化传感器的安装位置。通过谐波响应分析（Harmonic Response Analysis），研究轮辐在不同频率下的应力分布与变形模式，以找出最优的传感器布置策略，使其在不增加计算成本的前提下，提供最高信噪比的地形识别信号。

在低频（90Hz）振动模式下，轮毂的整体变形较大，主要用于检测大尺度地形起伏（如陡坡、深坑）。分析发现，在该频率范围内，轮辐边缘的振幅最大，意味着该区域的信号能量最强，适合布置传感器以捕获整体振动趋势。而在中高频（200-300Hz）振动模式下，轮毂表现出明显的局部共振现象，振动响应集中在轮辐的特定区域，这些共振区域对小型石块、粗糙表面的细节感知更加敏感。因此，在传感器布置上，我们需要针对这两个不同频段的特点，在低频模式下将传感器安装于轮辐边缘，而在高频模式下则放置在局部共振区域，以确保对不同尺度地形特征的有效识别。

轮辐振动特性分析

轮辐作为机器人轮毂的重要支撑结构，在机器人行进过程中受到来自地面的激励，产生不同方向的应力和变形。图（A）展示了水平和垂直方向上的作用力随时间的变化，其中水平方向的冲击力更显著，而垂直方向的力在后期逐渐增强，这说明轮辐结构会经历复杂的振动响应。由于轮辐连接部位与轮胎直接相连，该部分会优先传导地面的冲击力，并产生局部的应力集中，因此对轮辐的受力分析是优化传感器布置的关键。

为了进一步分析不同工况下的应力分布，我们对轮辐进行了两种不同的加载方式。第一种情况（B 图）为低频振动模式，主要模拟缓慢行驶或大尺度地形起伏的情况，此时轮辐整体受力较为均匀，最大应力达到 10.524 MPa，主要集中在轮辐的下部支撑区域。第二种情况（C 图）为高频激励模式，模拟机器人快速滚动通过碎石或粗糙地形的情境，结果显示最大应力提高至 16.707 MPa，且应力集中区域向轮辐的连接部位转移。这一分析表明，低频模式下的应力较均匀，而高频模式下应力局部化更加显著，高应力区域可以作为传感器的最佳布置位置。

变形与应力时序分析

在传感器布置优化过程中，我们选取了三个不同的位置（D 图），并对其应力与变形随时间的变化进行了对比分析。首先，在应力变化趋势（E 图）中，不同传感器位置的应力变化存在明显差异。位置 1（黄色）的初始应力较高，但快速衰减，表明该区域主要受到低频激励影响，适用于检测坡度变化或大尺度障碍物。位置 2（橙色）的应力较为稳定，表明该区域受力更加均匀，适用于捕获多频段信息。位置 3（蓝色）的应力在后期波动较大，表明该区域可能是高频信号的良好捕捉点。

在变形响应分析（F 图）中，三个传感器位置的形变幅度也有所不同。位置 1 的变形最大，初始阶段的形变达到 30mm，表明该区域对低频信号最敏感。位置 2 的变形较均衡，能够捕获不同频率的信号变化。位置 3 的变形最小，但仍然可以反映高频信号的传播特性。这一结果表明，不同传感器布置点能够获取不同尺度的地形信息，需要结合具体任务需求选择最佳布置位置。

信号增益分析

在传感器信号处理过程中，应力-变形增益（Gain）是一个重要的评价指标，它反映了应力对变形的放大效应。图（G）展示了三个位置的增益随时间的变化趋势，其中位置 1（黄色）的增益在初期较低，但后期突然上升，说明该区域在低频激励下可能对某些特定地形更加敏感。位置 2（橙色）的增益较为稳定，适用于综合测量不同地形的特征。位置 3（蓝色）的增益在短时间内急剧上升，表明该区域对高频振动的响应较为强烈，可以用于识别小尺度的地形变化。

从增益分布来看，低频模式下信号的放大效应较弱，而高频模式下的信号增益明显更大，这意味着高频振动可以在局部区域产生更强的共振，使传感器能够检测更精细的地形特征。因此，结合信号增益分析，传感器的布置需要在不同频段下兼顾应力与变形的综合响应，以提高地形识别的准确度。

香农熵分析：信号信息量优化

为了进一步优化传感器的布置，我们计算了 Shannon 熵值（K 图），用于衡量各个点的信号复杂度。Shannon 熵值越高，说明信号包含的信息越丰富，能够提供更详细的地形特征。结果显示，位置 1 的 Shannon 熵值最低，表明该区域的信号变化较小，适用于检测平稳或低频地形特征。位置 2 的 Shannon 熵值处于中等水平，适合用于多频段的信号测量。位置 3 的 Shannon 熵值最高，说明该区域的信号变化最剧烈，适合捕获高频信号，识别细小的地形特征。这一分析表明，高熵值区域更适合传感器布置，以获取最丰富的地形信息。

传感器布置优化结论

结合 FEA 计算的应力分析、变形响应、信号增益分析以及 Shannon 熵计算，我们最终确定了三个最佳的传感器布置点：

位置 1（轮辐顶部）：适用于低频振动测量，检测大尺度地形特征。
位置 2（轮辐内侧中部）：多频段测量点，提供综合地形信息。
位置 3（轮辐底部连接点）：高频信号测量点，检测碎石、砂砾等小尺度地形。

为了提高信号质量，我们采用橡胶缓冲 + 螺丝固定的方式安装传感器，以减少高频振动干扰，提高长期测量的稳定性。

传感器选择

在本研究中，针对轮辐振动信号的特点，系统性地评估并选择了最适合的传感器类型，以满足高精度、低功耗、实时性的地形识别需求。传感器选型过程中，重点考虑了信号检测范围、灵敏度、频率响应、功耗以及安装方式等因素。由于轮辐振动信号覆盖低频（<100Hz）、中频（100-300Hz）和高频（>500Hz），所选传感器需要具备宽频带响应能力，以确保完整捕获不同地形特征。此外，地形特征的变化可能导致微小的振动信号，因此传感器需具有高灵敏度，能够有效检测微弱的机械波动。

本研究的传感器选型策略确保了信号灵敏度、频率响应、功耗控制和数据质量的平衡，最终采用的压电振动传感器能够有效捕捉轮辐的振动特性，提高地形识别系统的准确性。

机器人测试平台

为了保证数据采集的可靠性，我们在实验室环境下搭建了一个标准化的测试平台。该平台主要包括：

1:4 缩比的 Curiosity 火星探测车轮毂，用于模拟真实的地形滚动环境。
三组压电振动传感器，安装在轮辐顶部、轮辐内侧中部和轮辐底部连接点，用于捕捉不同区域的振动信号。
高精度数据采集卡（DAQ），用于采集传感器信号，并以1 kHz 采样率记录数据。
多种地形样本，包括平坦地面、砂砾、小石块、粗糙表面和陡坡，用于测试不同地形对振动信号的影响。

为了模拟实际运行环境，我们采用恒速驱动系统，以控制机器人轮子的滚动速度。实验过程中，我们设定多个速度级别，以测试不同滚动速度对振动信号的影响。此外，为了降低外部噪声的干扰，我们在实验室内使用隔震平台，确保采集到的振动信号尽可能纯净，不受外界干扰影响。

初步实验分析总结

本研究对小石块地形、沙地和平坦地面三种不同地形进行了初步实验，并通过FFT 频谱分析与特征值（Eigenvalue）分析评估了压电传感器的性能。实验采用 Arduino Mega 进行数据采集，采样频率为 720 Hz，每种地形共采集 9500 组数据。

1. FFT 频谱分析，图1

FFT 频谱分析（图 \ref{FFT}）显示，不同地形的振动信号具有明显的频率特征，与有限元分析（FEA）预测结果高度一致，验证了模型的准确性：

小石块地形（A）：由于石块尺寸不均匀，信号主要集中在低频（0-50 Hz）和中频（~200 Hz），其中位置 2 在 200 Hz 处有显著峰值。
沙地（B）：沙粒较小且密集，振动信号主要表现为高频成分（450-700 Hz），其中位置 3 传感器对高频响应最明显。
平坦地面（C）：地面均匀，振动信号幅度低，所有频率范围内的振动特征较弱。

FFT 结果表明，不同传感器位置对不同频段的振动敏感度不同：位置 1 适用于低频（0-50 Hz），位置 2 对中频（~200 Hz）敏感，位置 3 捕捉高频（450-700 Hz）信号。这些发现不仅验证了 FEA 预测结果，同时也支持 Shannon 熵分析，表明传感器能够有效捕获不同地形的特征频率，具有较好的地形分类潜力。

2. 特征值（Eigenvalue）分析，图2

特征值分析（图 \ref{eigen}）基于传感器输出的 3×3 协方差矩阵，用于评估不同地形的振动信号方差与相关性。实验结果表明：

小石块地形的特征值分布最分散，方差较大，反映出地形的不规则性和强烈的振动变化。
沙地的特征值适中，表现为半均匀的特性，振动信号方差介于小石块和平坦地面之间。
平坦地面的特征值最小且高度聚集，表明信号稳定性高，振动变化最小。

特征值分布进一步揭示了地形复杂度与振动能量的关系，即：小石块地形的特征值最大，表明振动能量最高；平坦地面最小，表明地形稳定性强；沙地处于两者之间。此外，特征值的 2D 投影清晰区分了三种地形，支持基于机器学习（如 k-NN、SVM）的分类方法，并进一步表明较大特征值对应更剧烈的地形动态交互，而较小特征值代表更稳定的地面状态。

3. 结论

实验结果表明，FFT 频谱分析与特征值分析能够有效区分不同地形，并且与 FEA 预测结果一致，证明了所选压电传感器的可行性。不同地形在频域和特征值空间中具有明显的可分性，为后续基于机器学习的地形分类提供了强有力的数据支持。此外，本研究验证了传感器位置优化的有效性，进一步确认了不同传感器位置对不同频率信号的敏感性。未来，我们将基于这些实验结果优化信号处理算法，并构建机器学习模型，实现更精确的地形识别和分类。

特征提取

在初步分析中，我们已验证不同地形的振动信号在频域上具有明显的差异。下一步，我们进行特征提取与机器学习建模，以实现高效的地形分类。特征提取的目标是捕获各频率范围内的振动响应，并从**轮辐的三个传感器位置（低频、中频、高频）**提取特征，确保模型能够充分学习不同地形的信号模式。

每个传感器位置对特定频率范围敏感：

位置 1（低频 1–50 Hz）：捕捉地形顺应性和整体变形特性
位置 2（中频 50–300 Hz）：分析振动的周期性和变化平稳性
位置 3（高频 400–800 Hz）：检测微小地形不规则性和表面粗糙度

这些特征经过优化，以增强地形分类模型的性能，详细分析如下。

1. 位置 1 传感器特征（低频 1–50 Hz）

位置 1 主要用于检测低频振动分量，这些信号与地形的顺应性（Compliance）和整体刚度（Stiffness）有关。

低频均方根值（Low-Frequency RMS）
RMS 衡量低频信号的能量，反映地形的顺应性：

低 RMS 值通常对应于软质地形（如沙地），而高 RMS 值则表明地形较硬（如岩石地面）。
低频标准差（Low-Frequency Standard Deviation）
该指标衡量信号的波动程度，用于评估地形的均匀性：

标准差较大表明地形变化剧烈，例如石块地形；标准差较小则对应均匀的表面，如沙地或平坦地面。

结论：位置 1 适用于评估地形整体刚度和顺应性，低频 RMS 和标准差可用于区分沙地（低值）与岩石地形（高值）。

位置 2 传感器特征（中频 50–300 Hz）

位置 2 主要用于分析地形的周期性和振动稳定性，适用于识别规则排列的石块或颗粒状地形。

自相关峰值（Autocorrelation Peak）
该指标用于衡量信号的周期性，可用于识别地形模式，例如均匀排列的石块：

如果某个频率处的自相关峰值较高，意味着该地形具有重复性特征，如规则排列的鹅卵石。
振幅变化平稳度（Smoothness of Amplitude Variation）
该特征用于评估振幅变化的平滑程度，表明地形过渡的平稳性：

高平稳度值表示地形变化较平滑（如沙地），低平稳度值表示地形变化剧烈（如岩石地形）。

结论：位置 2 适用于评估地形的振动周期性，能够识别规则排列的石块（高自相关）和沙地（高振幅平稳度）。

位置 3 传感器特征（高频 400–800 Hz）

位置 3 主要用于检测微小的地形不规则性，如表面粗糙度、碎石等小障碍物。

高频标准差（High-Frequency Filtered Standard Deviation）
该指标用于测量高频信号的波动情况，以评估表面粗糙度：

标准差越大，表明地形越不均匀，例如石块较多的表面；标准差较小，则表明地形较光滑。
峰度（Kurtosis, Spike Rate）
峰度用于识别信号中尖锐的瞬态峰值，以检测微小障碍物：

高峰度值表示信号中存在大量短时间内的剧烈冲击（如崎岖地面），而低峰度值表明地形较为平滑（如平坦地面）。

结论：位置 3 适用于检测表面粗糙度和小障碍物，可用于区分崎岖地形（高峰度）和光滑表面（低峰度）。

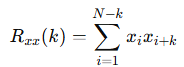
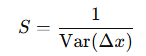
结果分析

为了验证所提出的方法，我们进行了地形识别实验，通过安装在机器人轮辐上的压电传感器，采集六种不同地形的振动数据，并基于不同频率范围的特征进行分析。实验目标是评估所提取特征在机器学习模型中的表现，并验证基于压电传感器的振动信号分类方法的有效性。

1. 地形数据采集与分类实验

本研究使用六种地形进行分类实验（图 9）：
(A) 平坦地面（Flatterrain）
(B) 细沙地形（Finesandyterrain，粒径 <1mm）
(C) 小石块地形（SmallStone terrain，粒径 5-10mm）
(D) 小鹅卵石地形（SmallPebble terrain，粒径 20-30mm）
(E) 大石块地形（LargeStone terrain，粒径 50-70mm）
(F) 未知地形（Unknown terrain，由沙地和小石块混合组成）

振动信号的特征提取基于低、中、高频段分析，分别对应轮辐不同传感器位置，以捕获各地形的独特振动模式。实验数据用于支持向量机（SVM）分类，评估地形识别的准确性。

2. SVM 分类结果

本研究使用支持向量机（SVM）模型对前五种已知地形（A-E）进行分类，并在未知地形（F）上测试泛化能力。分类模型的输入特征包括：

均方根值（RMS）
标准差（STD）
峰度（Kurtosis）
偏度（Skewness）
信号能量（Signal Energy）
熵（Entropy）

这些特征分别针对低频（1-50Hz）、中频（50-300Hz）、高频（400-800Hz）进行计算，以确保模型能够准确捕获地形的振动特征。

3. 结果分析

采用 1.5 秒时间窗口（对应 2000 行数据）进行分类，机器人移动速度为 67 mm/s，采样频率为 1440 Hz。
分类准确率达 90%，表明压电传感器振动信号能够有效用于地形识别。
混淆矩阵（图 10）显示，各地形之间的分类具有清晰的边界：
- 小石块、小鹅卵石和平坦地面分类准确率达 100%，表明这些地形的振动信号模式明显不同，易于识别。
- 大石块地形和沙地分类准确率较低，可能由于机器人在大石块上滑动导致振动频率增加，使其特征与沙地重叠，降低了分类精度。

结论：尽管仅使用六个统计特征，SVM 模型仍然能高效区分不同地形，表明基于频域特征提取 + 机器学习分类的方法在计算资源受限的情况下仍然具有较高的识别效率。

未知地形的表面粗糙度估计

表面粗糙度是影响地形振动特征的关键因素，不同的地形会产生不同的振动模式，因此，估计地形的表面粗糙度有助于识别未知地形。本研究基于低、中、高频信号的 RMS、标准差（STD）和峰度（Kurtosis）等特征，构建地形特征矩阵，用于衡量地形之间的相似性。对于已知地形，我们计算其平均特征向量作为参考基准，而未知地形的特征向量则用于相似度匹配，以推测其最可能的类别。

1. 计算地形相似性的方法

为了提高未知地形分类的准确性，我们采用了两种互补的距离度量方法：

欧几里得距离（Euclidean Distance）：衡量特征向量在几何空间上的直线距离
马哈拉诺比斯距离（Mahalanobis Distance）：考虑特征间的统计依赖关系

2. 欧几里得距离 vs. 马哈拉诺比斯距离

欧几里得距离假设所有特征相互独立且权重均等，因此它仅关注特征向量在几何空间中的接近程度，适用于特征分布较均匀的情况。
马哈拉诺比斯距离则考虑了特征之间的相关性，能够根据数据的分布情况调整不同特征的权重，从而避免单个特征过度主导分类结果，尤其适用于高度相关的振动信号数据。

结论：欧几里得距离能够快速计算地形的几何相似度，但在地形振动信号特征存在统计相关性的情况下，马哈拉诺比斯距离可以提供更加可靠的分类结果。因此，结合两种距离方法能够提高未知地形估计的稳健性

3. 未知地形分类结果

如图 11 所示，我们计算了未知地形与五种已知地形的距离：

欧几里得距离（图 11A）结果表明，未知地形与小石块地形（Small Stone）最接近（值：0.2535），表明它在几何特征上更接近小石块。
马哈拉诺比斯距离（图 11B）显示未知地形与沙地（Sand）具有更大的统计相似性（值：1.8759），表明其信号特征在统计分布上更接近沙地。

结论：

欧几里得距离更关注地形形态相似性，表明未知地形的振动信号幅值更接近小石块地形。
马哈拉诺比斯距离考虑了特征的统计相关性，表明未知地形的振动模式可能受到沙地特征的影响。
由于未知地形是沙地与小石块的混合地形，两种度量方法给出的结果具有互补性，因此结合两种方法可以更准确地估计未知地形的类别。

研究总结

本研究提出了一种基于振动信号的地形识别方法，使用压电传感器采集不同地形的振动信号，通过提取低、中、高频特征并结合支持向量机（SVM）进行分类，成功实现了对已知地形（如沙地、小石块等）的高精度识别，分类准确率达到90%。此外，针对未知地形的表面粗糙度估计，我们结合欧几里得距离与马哈拉诺比斯距离，有效量化了地形相似性。实验结果表明，本方法在低计算资源的情况下，能够快速且准确地进行地形分类，具有较强的实际应用潜力。

← BACK TO PROJECTS